ZP2CAS

Purpose:

Converts zeros, poles and gain to cascade form filter coefficients.

Syntax:

ZP2CAS(z, p, k, "flag")

A series, the zeros.

A series, the poles.

Optional. A scalar, the gain. Defaults to 1.0.

"flag"

Optional. A string, the stage ordering flag:

"up"	:	order stages such that the poles of each stage are closer to the unit circle than the previous stage (default)
"down"	:	order stages such that the poles of each stage are closer to zero than the previous stage

Returns:

A series, the system coefficients in cascaded biquad form.

Example:

z = {0.0, 2.0};

p = {0.5, 0.2};

k = 1.0;

c = zp2cas(z, p, k);

c == {1, 1, -2, 0, -0.7, 0.1};

The 2nd order cascade filter coefficients represent the following Z transform:

Remarks:

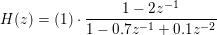
ZP2CAS converts the zeros, poles and gain of a discrete system to cascade coefficient form where the coefficients represent the following Z transform:

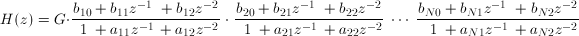
or:

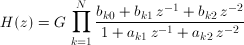
where G is the system gain, b_k and a_k are the filter coefficients for the k^th stage.

The cascade filter coefficients are returned as a single column series with the coefficients in the following order:

{G, b₁₀, b₁₁, b₁₂, a₁₁, a₁₂, b₂₀, b₂₁, b₂₂, a₂₁, a₂₂, ... , b_N0, b_N1, b_N2, a_N1, a_N2}

CAS2ZP also works for analog cascade coefficients. In this case, the cascade system function becomes:

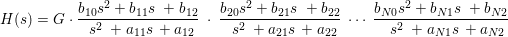
or equivalently:

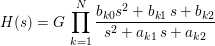
To yield real coefficients, the zeros and poles must occur in complex conjugate pairs or be real.

The stages are ordered such that the poles of each stage are closer to the unit circle than the previous stage. The zeros of each stage are chosen to be closest to the poles of the same stage.

If "flag" == "down", the stages are reversed.