DADiSP Online Help

Click here to see this page in full context

TF2CAS

Purpose:

Converts transfer function form filter coefficients to cascade form.

Syntax:

TF2CAS(b, a)

(num, den, gain) = TF2CAS(b, a)

Returns:

A series, the cascade form of the filter coefficients.

(num, den, gain) = TF2CAS(b, a) returns the numerator and denominator cascade coefficients as separate Nx3 arrays where each row represents a 2nd order stage. The gain is returned as a separate scalar.

Example:

b = {1};

a = {1, -0.5, 0.2};

c = tf2cas(b, a)

c == {1, 1, 0, 0, -0.5, 0.2}

The direct form filter coefficients represent the following Z transform:

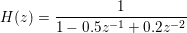
The resulting 2nd order cascade coefficients represent the equivalent Z transform:

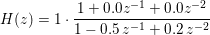
Since the original coefficients represent a single 2nd order system, the cascade denominator coefficients are identical.

Example:

b = {1};

a = {1, -0.5, 0.2, 0.1};

c = tf2cas(b, a);

c == {1, 1, 0, 0, -0.754856, 0.392379, 1, 0, 0, 0.254856, 0}

The direct form filter coefficients represent the following Z transform:

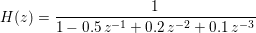
The resulting 2nd order cascade coefficients represent the equivalent Z transform:

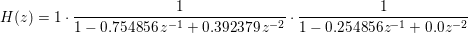
The direct form coefficients are represented by two stages of 2nd order cascade coefficients.

Example:

b = {1};

a = {1, -0.5, 0.2, 0.1};

(num, den, gain) = tf2cas(b, a);

num == {{1, 0, 0},

        {1, 0, 0}}

den == {{1, -0.754856, 0.392379},

        {1,  0.254856, 0.0}}

gain == 1

Same as the previous example except the cascade coefficients are returned as separate 2x3 arrays where each row represents the coefficients of a 2nd order stage.

Remarks:

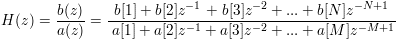
For tf2cas(b, a), the input series represent the terms of the rational polynomial H(z) = b(z) / a(z) where:

The cascade form of the coefficients represent the equivalent Z transform:

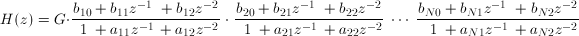
or:

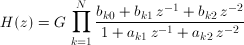
where G is the system gain, b_k and a_k are the filter coefficients for the k^th stage.

The cascade filter coefficients are returned as a single column series with the coefficients in the following order:

{G, b₁₀, b₁₁, b₁₂, a₁₁, a₁₂, b₂₀, b₂₁, b₂₂, a₂₁, a₂₂, ... , b_N0, b_N1, b_N2, a_N1, a_N2}

The cascade form of the filter coefficients can be processed by the CASCADE function. Filtering with cascade form coefficients can reduce numerical roundoff errors compared to the same filtering operation in direct form.

See CAS2TF to convert cascade coefficients to direct form.

See Also:

CAS2TF

CAS2ZP

DADiSP/Filters

RESIDUEZ

ROOTS

TF2SOS

TF2ZP

TF2ZPK

ZFREQ

ZPLANE