TF2ZPK

Purpose:

Converts Z plane transfer function form to zeros, poles and gain.

TF2ZPK(b, a)

(z, p, k) = TF2ZPK(b, a)

b	-	A series. The numerator (i.e. zero) coefficients in ascending powers of z^-1.
a	-	A series. The denominator (i.e. pole) coefficients in ascending powers of z^-1.

A Nx3 array where the first column contains the zeros, the second column contains the poles and the third column contains the gain.

(z, p, k) = TF2ZPK(b, a) returns the zeros, poles and gain as three separate arrays.

$image\zplane01.gif$

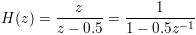
W1: tf2zpk({1}, {1, -0.5})

W1 contains three columns, where the first column is a zero at 0.0, the second column is a pole at 0.5 and the third column is the gain of 1.0.

(z, p, k) = tf2zpk({1}, {1, -0.5});

z == {0.0}

p == {0.5}

k == 1.0

Same as above except the values are returned in three separate variables.

$image\zplane02.gif$

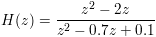
b = {1, -2, 0};

a = {1, -0.7, 0.1};

(z, p, k) = tf2zpk(b, a);

z == {0.0, 2.0}

p == {0.5, 0.2}

k == 1.0

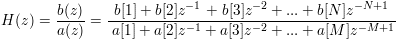
For tf2zpk(b, a), the input series represent the terms of the rational polynomial H(z) = b(z) / a(z) where:

$image\zplane03.gif$

See TF2ZP to convert a continuous S plane transfer function to zeros, poles and gain.

See ZP2TF to convert zeros, poles and gain to transfer function form.