CAS2ZP

Purpose:

Converts cascade form filter coefficients to zeros, poles and gain.

CAS2ZP(c)

(z, p, k) = CAS2ZP(c)

A series. The filter coefficients in cascade form.

A Nx3 array where the first column contains the zeros, the second column contains the poles and the third column contains the gain.

(z, p, k) = CAS2ZP(c) returns the zeros, poles and gain as three separate arrays.

c = {1, 1, -2, 0, -0.7, 0.1};

W1: cas2zp({1, 1, -2, 0, -0.7, 0.1})

W1 == {{0.0, 0.5, 1.0},

{2.0, 0.2}}

The 2nd order cascade filter coefficients represent the following Z transform:

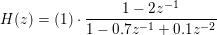
The first column of W1 contains the zeros, the second column contains the poles and the third column is the gain.

c = {1, 1, -2, 0, -0.7, 0.1};

(z, p, k) = cas2zp(c);

z == {0.0, 2.0};

p == {0.5, 0.2};

k == 1.0;

The 2nd order cascade filter coefficients represent the following Z transform:

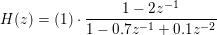
Same as the previous example except z contains the zeros, p contains the poles and k is the gain of the system.

CAS2ZP converts cascade coefficients to zeros, poles and gain of a discrete system where the input coefficients represent the following Z transform:

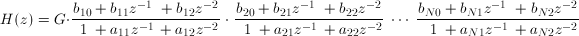
or:

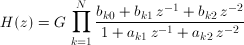
where G is the system gain, b_k and a_k are the filter coefficients for the k^th stage.

The cascade filter coefficients are returned as a single column series with the coefficients in the following order:

{G, b₁₀, b₁₁, b₁₂, a₁₁, a₁₂, b₂₀, b₂₁, b₂₂, a₂₁, a₂₂, ... , b_N0, b_N1, b_N2, a_N1, a_N2}

CAS2ZP also works for analog cascade coefficients. In this case, the cascade system function becomes:

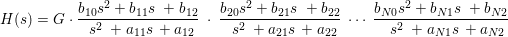
or equivalently:

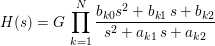
See ZP2CAS to convert zeros, poles and gain to cascade form.