KWLPASS

Purpose:

Designs an FIR linear phase Kaiser lowpass filter.

Syntax:

KWLPASS(order, rate, fc, fstop, attn, "unity_dc")

order	-	Optional. An integer, the filter length. If not specified, the filter order is automatically estimated.
rate	-	A real, the sample rate of the filter in Hertz.
fc	-	A real, the cutoff frequency in Hertz.
fstop	-	A real, the stopband frequency in Hertz.
attn	-	A real, the stopband attenuation in dB.
"unity_dc"	-	Optional. A string, "unity_dc" explicitly sets f(0) to 1.0

Returns:

A series, the lowpass filter coefficients. The filter coefficients are identical to the impulse response of the FIR filter.

Example:

W1: kwlpass(1000.0, 200.0, 250.0, 60.0)

W2: 20*log10(filtmag(W1, {1}, 1024))

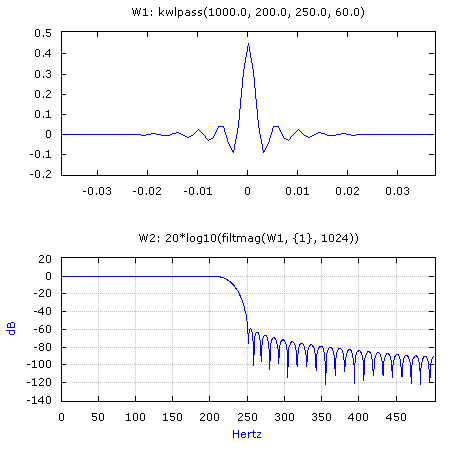
Generates a 75 point lowpass filter with a pass band edge of 200 Hz and a stop band edge of 250 Hz. The stopband attenuation is 60 dB and the time offset is -0.037 seconds. W2 displays the frequency response of the filter.

Example:

W1: kwlpass(1000.0, 200.0, 250.0, 60.0)

W2: gsin(1000, 1/1000, 10) + gsin(1000, 1/1000, 400)

W3: firfilterf(W2, W1)

Generates the same FIR lowpass filter as the previous example. W2 contains a series with two sinusoids and W3 applies the filter to recover the low frequency sinewave.

Example:

W2: kwlpass(90, 1000.0, 200.0, 250.0, 60.0)

Designs the same filter as above except the filter order is explicitly set to 90 samples resulting in a slightly narrower transition band.

Example:

W3: kwlpass(90, 1000.0, 200.0, 250.0, 60.0, "unity_dc")

Same as above except the DC frequency response value, f(0), is explicitly set to 1.0 (0.0 dB).

Remarks:

The KWLPASS filter specifications are depicted as follows:

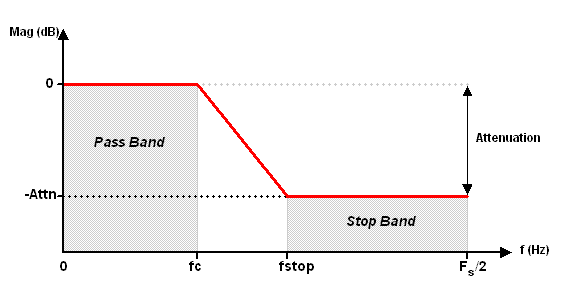
KWLPASS designs a lowpass filter using a Kaiser window method. The impulse response of the ideal filter is multiplied by a Kaiser window to produce a linear phase FIR filter with a flat passband. The filter is non-causal and time symmetric about t = 0 and the offset is equal to:

- (length-1) / (rate * 2)

The filter order refers to the number of resulting filter coefficients.

The optional "unity_dc" flag guarantees the resulting filter has a frequency response of 1.0 (i.e. 0 dB) at f(0).

The lowpass edges must lie between 0.0 and 0.5 * rate (the Nyquist frequency). Overlapping band edges are not permitted.

Although a filter designed with the Kaiser window method exhibits a flat passband response, the resulting filter generally has more coefficients than the Remez Exchange method. See LOWPASS to design a linear phase FIR lowpass filter using the Remez Exchange algorithm.

See BESSEL, BUTTERWORTH, CHEBY1, CHEBY2 and ELLIPTIC to design IIR filters using the Bilinear Transform method.

KWLPASS requires the DADiSP/Filters Module.

References:

Oppenheim and Schafer

Discrete Time Signal Processing

Prentice Hall, 1989

Digital Signal Processing Committee

Programs for Digital Signal Processing

I.E.E.E. Press, 1979

Bateman & Yates

Digital Signal Processing Design

Computer Science Press, 1989

KWLPASS

Purpose:

Syntax:

Returns:

Example:

Example:

Example:

Example:

Remarks:

See Also:

References: