KAISER

Purpose:

Multiplies a series with a Kaiser window.

Syntax:

KAISER(series, ampflag, beta)

series

A series or array.

ampflag

Optional. An integer, the amplitude correction flag:

0	:	do not correct amplitude (default)
1	:	correct amplitude
2	:	correct RMS amplitude
3	:	correct mean squared amplitude

beta

Optional. A real, the scaling factor. Defaults to 7.865.

Alternate Syntax:

KAISER(N, ampflag, beta)

An integer, the window length.

ampflag

Optional. An integer, the amplitude correction flag:

0	:	do not correct amplitude (default)
1	:	correct amplitude
2	:	correct RMS amplitude
3	:	correct mean squared amplitude

beta

Optional. A real, the scaling factor. Defaults to 7.865.

Returns:

A series or array.

Example:

W1: gsin(1000, .001, 45)

W2: spectrum(kaiser(W1))

W3: spectrum(kaiser(W1, 1))

The MAX of W2 == 0.4389 and the MAX of W3 == 1.0. The amplitude of the spectrum in W3 has been corrected to take into account amplitude effects of the Kaiser window.

Remarks:

If ampflag == 1, the correction factor is the mean of the spectral window. This assures that the spectrum of a sinusoid of amplitude A has a peak of A.

If ampflag == 2, the correction is applied as follows:

w = kaiser(s) * rms(s) / rms(kaiser(s))

This assures that:

sqrt(area(psd(w))) == rms(s) approximately

If ampflag == 3, the correction is applied as follows:

w = winfun(s) / sqrt(mean(win * win)

where win is the windowing function.

The Kaiser window is generated using the following formula:

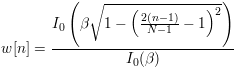
where n is the n^th point (1 <= n <= N), I_o is the modified zeroth order Bessel function of the first kind. Default β is 7.865 and N is the number of points to generate.

See GKAISER to generate a Kaiser window.