DADiSP Online Help
Click here to see this page in full context

DADiSP Worksheet Functions > Function Categories > Fourier Transforms and Signal Processing > WINFUNC
Multiplies a series with a spectral window.
WINFUNC(func, series, ampflag, beta, "sym")
|
func |
- |
An integer, the windowing function. Valid inputs are:
|
||||||||||||||||||||
|
series |
- |
A series or array. |
||||||||||||||||||||
|
ampflag |
- |
Optional. An integer, the window correction method.
|
||||||||||||||||||||
|
beta |
- |
Optional. A real, beta value for the Kaiser window. Defaults to 7.865. For a Flattop window, beta determines the Flattop window coefficients. For a |
||||||||||||||||||||
|
"sym" |
- |
Optional. A string, the window symmetry flag.
|
A series or array.
W1: gsin(1000, .001, 45)
W2: spectrum(winfunc(0, W1))
W3: spectrum(winfunc(0, W1, 1))
The MAX of W2 == 0.539 and the MAX of W3 == 1.0. The amplitude of the spectrum in W3 has been corrected to take into account amplitude effects of the Hamming window.
WINFUNC is the core routine for the BLACKMAN, BLACKMANHARRIS, FLATTOP, HAMMING, HANNING and KAISER SPL functions.
If ampflag == 1, the correction factor is the mean of the spectral window. This assures that the spectrum of a sinusoid of amplitude A has a peak of A.
If ampflag == 2, the correction is applied as follows:
w = winfun(s) * rms(s) / rms(winfun(s))
where winfun is Blackman, Blackmanharris, Flattop, Hamming, Hanning or Kaiser. This assures that:
sqrt(area(psd(w))) == rms(s) approximately
If ampflag == 3, the correction is applied as follows:
w = winfun(s) / sqrt(mean(win * win)
where win is the windowing function.
The "sym" flag controls the window symmetry as follows:
"Symmetric" (the default) removes any leading and trailing zeros. For an N point symmetric window, a N-1 point periodic window is effectively created and the Nth point is set to the same value as the first point. For the Hanning window, a N+1 point periodic window is created and the trailing zero is removed.
"Periodic" or "iso" creates a periodic window function useful in spectrum analysis applications where the starting zero is preserved and the trailing zero is removed. "Periodic" or "iso" conforms to the ISO 18431-1 standard for windowing functions.
"Direct" implements the core window function where any leading and trailing zeros are preserved. This mode is the same as "symmetric" for all windows except Hanning.
"Sym" defaults to "periodic" for Flattop and "symmetric" for all other windows.
For a Taylor window, this flag is a real and sets the stopband attenuation.
The Hamming, Hanning, Flattop and Blackman windows are part of the family of cosine window functions. The ISO 18431-1 standard periodic form of these windowing functions are defined by:
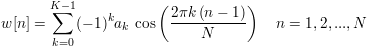
where K is the number of window coefficients and N is the length of the window. The symmetric form of the window can be constructed by setting N to N-1. For the symmetric Hanning window, a N+1 periodic window is created and the trailing zero is removed.
For the cosine windows, the default coefficients are as follows:
Hamming:
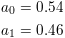
Hanning:
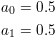
Flattop:
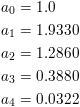
Blackman:
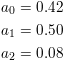
Blackman-Harris: