DADiSP Online Help
Click here to see this page in full context

DADiSP Worksheet Functions > Function Categories > Fourier Transforms and Signal Processing > HAMMING

 

HAMMING

Purpose:

Multiplies a series with a Hamming window.

Syntax:

HAMMING(series, ampflag, "sym")

series

-

A series or array.

ampflag

-

Optional. An integer, the amplitude correction flag:

0

:

do not correct amplitude (default)

1

:

correct amplitude

2

:

correct RMS amplitude

3

:

correct mean squared amplitude

"sym"

-

Optional. A string, the symmetry flag:

"symmetric"

:

Starting and ending points are equal, but leading and trailing zeros are removed (default).

"periodic"

:

Periodically extended window where the leading zero is preserved. Conforms to the ISO standard.

"iso"

:

Same as "periodic".

Alternate Syntax:

HAMMING(N, ampflag, "sym")

N

-

An integer, the length of the window.

ampflag

-

Optional. An integer, the amplitude correction flag:

0

:

do not correct amplitude (default)

1

:

correct amplitude

2

:

correct RMS amplitude

3

:

correct mean squared amplitude

"sym"

-

Optional. A string, the symmetry flag:

"symmetric"

:

Starting and ending points are equal, but leading and trailing zeros are removed (default).

"periodic"

:

Periodically extended window where the leading zero is preserved. Conforms to the ISO standard.

"iso"

:

Same as "periodic".

Returns:

A series or array.

Example:

W1: gsin(1000, .001, 45)

W2: spectrum(hamming(W1))

W3: spectrum(hamming(W1, 1))

 

The MAX of W2 == 0.539 and the MAX of W3 == 1.0. The amplitude of the spectrum in W3 has been corrected to take into account amplitude effects of the symmetric Hamming window. The symmetric window follows the form:

 

 

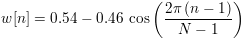
where n is the nth point (1 <= n <= N) and N is the number of points to generate. The leading and trailing zeros are preserved.

Example:

W4: hamming(1000, "periodic")

 

Creates a 1000 point periodic Hamming window that conforms to the ISO 18431-1 standard.

 

 

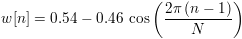
where n is the nth point (1 <= n <= N) and N is the number of points to generate. The leading and trailing zeros are preserved.

Remarks:

If ampflag == 1, the correction factor is the mean of the spectral window. This assures that the spectrum of a sinusoid of amplitude A has a peak of A.

 

If ampflag == 2, the correction is applied as follows:

 

 w = hamming(s) * rms(s) / rms(hamming(s))

 

This assures that:

 

sqrt(area(psd(w))) == rms(s) approximately

 

If ampflag == 3, the correction is applied as follows:

 

w = winfun(s) / sqrt(mean(win * win) 

 

where win is the windowing function.

 

The "sym" flag controls the window symmetry as follows:

 

"Symmetric" sets the last point to be the same value as the first point. For an N point symmetric window, a N-1 point periodic window is effectively created and the Nth point is set to the same value as the first point.

 

"Periodic" or "iso" creates a periodic window function useful in spectrum analysis applications. "Periodic" or "iso" conforms to the ISO 18431-1 standard for windowing functions.

 

The Hamming, Hanning, Flattop and Blackman windows are part of the family of cosine window functions. The ISO 18431-1 standard periodic form of these windowing functions are defined by:

 

 

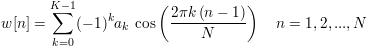
where K is the number of window coefficients and N is the length of the window. The symmetric form of the window can be constructed by setting N to N-1.

 

For the default Hamming window:

 

 

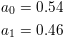
See GHAMMING to generate a Hamming window.

See Also:

BLACKMAN

BLACKMANHARRIS

CHEBWIN

FLATTOP

GHAMMING

HANNING

KAISER

PSD

SPECTRUM

TAYLORWIN

WINFUNC