
DADiSP Online Help
Click here to see this page in full context

DADiSP Worksheet Functions > Function Categories > Fourier Transforms and Signal Processing > BILINEAR
Converts a continuous system to a discrete system.
(Zd, Pd, Kd) = BILINEAR(Z, P, K, Fs, Fp)
|
Z |
- |
A series containing the zeros of the continuous transfer function. |
|
P |
- |
A series containing the poles of the continuous transfer function. |
|
K |
- |
A real. The gain constant. |
|
Fs |
- |
A real. The sampling frequency in Hertz. |
|
Fp |
- |
Optional. A real, the frequency in Hertz specifying at which point the frequency responses before and after mapping match exactly. |
(Ad, Bd, Cd, Dd) = BILINEAR(A, B, C, D, Fs, Fp)
|
A,B,C,D |
- |
Matrices containing the continuous state-space representation of the filter to be transformed. |
|
Fs |
- |
A real. The sampling frequency in Hertz. |
|
Fp |
- |
Optional. A real, the frequency in Hertz specifying at which point the frequency responses before and after mapping match exactly. |
(b, a) = BILINEAR(NUM, DEN, Fs, Fp)
|
NUM |
- |
A series containing the continuous numerator transfer function coefficients in descending powers of s. |
|
DEN |
- |
A series containing the continuous denominator transfer function coefficients in descending powers of s. |
|
Fs |
- |
A real. The sampling frequency in Hertz. |
|
Fp |
- |
Optional. A real, the frequency in Hertz specifying at which point the frequency responses before and after mapping match exactly. |
For the Zero-Pole-Gain format, two series and a constant. Zd is the vector of zeros, Pd is the series of poles, and Kd is the gain constant.
For the State-Space format, Ad, Bd, Cd and Dd are the state-space representations of the
For the Transfer Function format, b and a are series containing numerator and denominator transfer function coefficients.
b = {100};
a = {1, 2, 100};
(b1, a1) = bilinear(b, a, 200);
W1: (h, f) = sfreq(b, a, 1024);xy(f, mag(h))
W2: (h1, f1) = zfreq(b1, a1, 8192, 200);xy(f1, mag(h1))
W1 displays the magnitude of the frequency response for the continuous system:
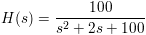
The system is converted to a digital system with a sample rate of 200 Hz where:
b1 == {0.000622, 0.001243, 0.000622}
a1 == {1.000000, -1.987570, 0.990056}
representing the system:
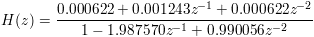
W2 displays the magnitude of the frequency response for the digital system.
(zd, pd, kd) = bilinear(roots(b), roots(a), 100, 200);
zd == {-1, -1}
pd == {0.993785 + 0.04947i, 0.993785 – 0.04947i}
kd == 0.000622
Same as the previous example except the inputs are given in Zero-Pole-Gain form. Note that:
b1 == poly(zd)*kd == {0.000662, 0.001243, 0.000662}
a1 == poly(pd) == {1.000000, -1.987570, 0.990056}
indicating the same discrete system is returned.
The bilinear transform converts a continuous, constant coefficient, time invariant analog system to a discrete, constant coefficient shift invariant digital system. In particular, the bilinear transform converts the analog system Ha (s) to a digital system Hd (z) with a sample period
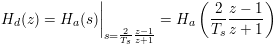
For continuous frequency Ω and normalized discrete frequency ω, the continuous frequency axis is mapped to the discrete unit circle such that:
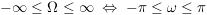
The relationship between Ω and ω can be seen with:
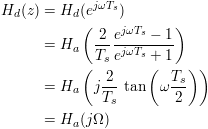
Thus, the mapping of continuous frequency Ω to discrete frequency ω and the inverse mapping become:

For the Zero-Pole-Gain format, BILINEAR maps the zeros Z, poles P and gain K of the continuous system to zeros Zd, poles Pd and gain Kd the discrete system.
For the State-Space format, BILINEAR maps the continuous state space matrices A, B, C, D where:
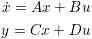
to the discrete state space matrices Ad, Bd, Cd, Dd where:
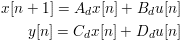
For the Transfer Function format, BILINEAR maps the continuous system
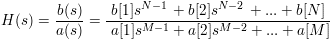

This form represents the following discrete difference equation:
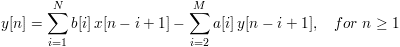
The bilinear transform of a stable continuous system always results in a stable discrete system.