DADiSP Online Help
Click here to see this page in full context

DADiSP Worksheet Functions > Function Categories > Special Functions > BESSELH

 

BESSELH

Purpose:

Evaluates the Bessel function of the third kind, the Hankel function for any real order.

Syntax:

BESSELH(v, K, z, opt)

v

-

A real or real series, the order. The order must be real but need not be an integer.

K

-

Optional. An integer, either 1 or 2. Specifies the type of the Hankel function. Defaults to 1.

z

-

Any scalar or series. The input value.

opt

-

Optional. An integer, the scaling method:

0:

no scaling (default)

1: 

scale by e-iz

2: 

scale by eiz

Returns:

A scalar or series, The value of Hν(K)(z) where ν is the order, z is the input and K is either 1 or 2, the type of Hankel transform.

Example:

besselh(0, 3)

 

returns -0.260052 + 0.376850i, the value of H0(1)(3).

Example:

W1: 0..0.2..1;

W2: besselh(1, 1, w1)

 

Returns H1(1)(z) for z between 0 and 1. W2 contains the series:

 

{NA,

 0.099501 - 3.323825i, 

 0.196027 - 1.780872i, 

 0.286701 - 1.260391i, 

 0.368842 - 0.978144i, 

 0.440051 - 0.781213i} 

Example:

besselh((3..9)', 0..0.2..10)

 

Evaluates the Bessel function of the third kind of type 1 for orders 3 through 9 with inputs from 0 to 10. Each column of the result contains the output for the specified order.

Remarks:

Bessel functions are solutions to the differential equation:

 

image\bessy01.gif

 

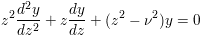
where ν is the order, Jν(z), is a solution of the first kind and Yν(z) is a linearly independent solution of the second kind.

 

The Hankel functions are related to the Bessel functions by:

 

image\bessh01.gif

 

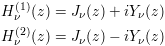
Hankel functions are also known as Bessel functions of the third kind.

 

BESSELH is based on a FORTRAN library written by D. E. Amos.

See Also:

AIRY

BESSELI

BESSELJ

BESSELK

BESSELY

JN

YN

References:

[1]   Abramowitz and Stegun

       Handbook of Mathematical Functions (9th printing 1970)

       US Gov. Printing Office

       Section 9.1.1, 9.1.89, 9.12

 

[2]   Amos, D.E.

       A Subroutine Package for Bessel Functions of a Complex

       Argument and Nonnegative Order

       Sandia National Laboratory Report

       SAND85-1018, May, 1985.

 

[3]   Amos, D.E.

       A Portable Package for Bessel Functions of a Complex

       Argument and Nonnegative Order

       Trans. Math. Software, 1986