DADiSP Online Help
Click here to see this page in full context

DADiSP Worksheet Functions > Function Categories > Special Functions > AIRY

 

AIRY

Purpose:

Evaluates the Airy function of the first or second kind.

Syntax:

AIRY(K, z)

K

-

Optional. An integer, the type of Airy function calculation.

0:

compute Ai(z), the Airy function of the first kind (default)

1:

compute the derivative of Ai(z)

2:

compute Bi(z), the Airy function of the second kind

3:

compute the derivative of Bi(z)

z

-

Any scalar or series. The input value, can be complex.

Returns:

A scalar or series, the value of Ai(z), Bi(z) or the derivatives.

Example:

airy(1.5)

 

returns 0.0717490, the value of Ai(1.5).

Example:

airy(2, 1.5)

 

returns 1.878942, the value of Bi(1.5).

Example:

x = -10..0.01..4;

ai = airy(0,x);

dai = airy(1,x);

bi = airy(2,x);

dbi = airy(3,x);

W1: ai;overp(bi,lred);sety(-1.5,1.5);label("Ai(x) and Bi(x)");

W2: dai;overp(dbi,lred);sety(-1.5,1.5);label("Derivative of Ai(x) and Bi(x)");

 

image\airy.gif

 

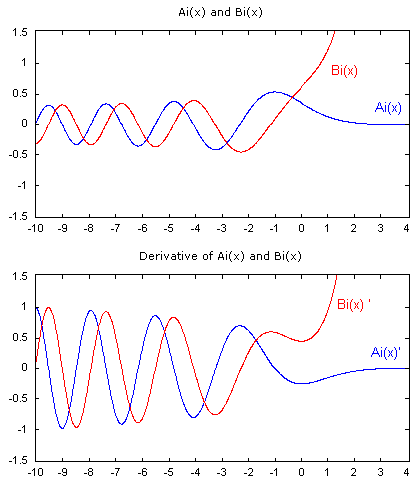
For x between –10 and 4, W1 displays the values of Ai(x) and Bi(x) and W2 displays the derivatives of Ai(x) and Bi(x).

Remarks:

Airy functions are solutions to the differential equation:

 

image\airy01.gif

 

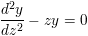
known as the Airy or Stokes equation. Ai(z) is a solution of the first kind and Bi(z) is a linearly independent solution of the second kind.

 

For positive values of x, the Airy functions are related to the modified Bessel functions by:

 

image\airy02.gif

 

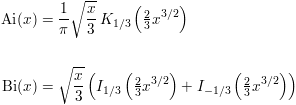
For negative values of x, the Airy functions are related to the Bessel functions by:

 

image\airy03.gif

 

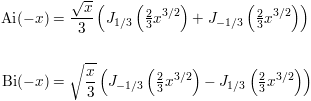
AIRY is based on a FORTRAN library written by D. E. Amos.

See Also:

BESSELI

BESSELJ

BESSELK

BESSELY

JN

YN

References:

[1]   Abramowitz and Stegun

       Handbook of Mathematical Functions (9th printing 1970)

       US Gov. Printing Office

       Section 9.1.1, 9.1.89, 9.12

 

[2]   Amos, D.E.

       A Subroutine Package for Bessel Functions of a Complex

       Argument and Nonnegative Order

       Sandia National Laboratory Report

       SAND85-1018, May, 1985.

 

[3]   Amos, D.E.

       A Portable Package for Bessel Functions of a Complex

       Argument and Nonnegative Order

       Trans. Math. Software, 1986