FADDEEVA

Purpose:

Evaluates w(z), the Faddeeva function.

FADDEEVA(z)

A scalar or series, the integration limit.

A scalar or series, the value of exp(z^-2) erfc(-iz).

faddeeva(1)

returns 0.367879 + 0.607158i, the value of:

exp(-1) * erfc(-i)

faddeeva(i)

returns 0.427584 + 0.000000i.

faddeeva((-2..0.01..2) * i);

xlabel("x");ylabel("w(x)");label("Faddeeva Function");

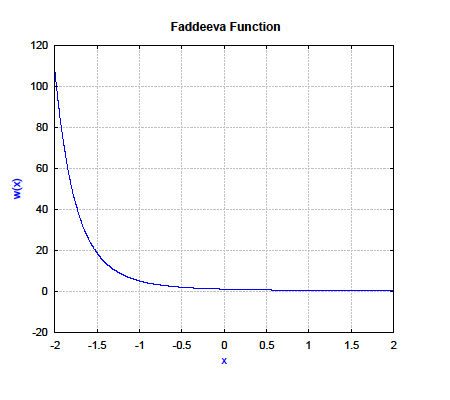
returns 401 samples of w(x).

W1: (-2..0.01..2) * i

W2: faddeeva(W1)

W3: exp(-(w1 * w1)) * erfc(-i * w1)

W2 contains the Faddeeva function and W3 computes the same function using exp(-z²) erfc(-iz).

The Faddeeva function, w(z), is defined as:

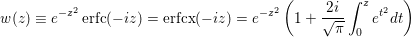
The input z may be complex.

The real and imaginary parts are decomposed as:

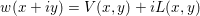
where V and L are the real and imaginary Voigt functions.

FADDEEVA is computed based on an algorithm developed by Steven G. Johnson.

The Faddeeva function is closely related to the DAWSON Integral.