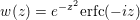DADiSP Online Help

Click here to see this page in full context

ERFI

Purpose:

Evaluates erfi(z), the imaginary error function.

Syntax:

ERFI(z)

Returns:

A scalar or series, the value of erfi(z) = -i erf(iz).

Example:

erfi(1)

returns 1.650426 the value of:

-i * erf(i)

Example:

erfi(1 + i)

returns 0.190453 + 1.316151i.

Example:

erfi(-2..0.01..2);

xlabel("x");ylabel("erfi(x)");label("Imaginary Error Function");

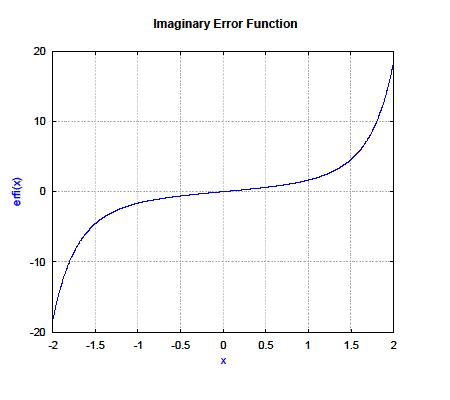
returns 401 samples of erfi(x).

Example:

W1: -2..0.01..2

W2: erfi(W1)

W3: -i * erf(i * w1)

W2 contains the imaginary error function and W3 computes the same function using  -i erf(iz).

Remarks:

The Imaginary Error Function, erfi(z), is defined as:

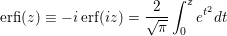
The input z may be complex.

ERFI is computed from the FADDEEVA function based on an algorithm developed by Steven G. Johnson. The Faddeeva function is defined as:

See Also:

ERF

ERFC

ERFCINV

ERFCX

ERFINV

FADDEEVA