SPECGRAM

Purpose:

Calculates the 2D joint time-frequency spectrogram as an image.

Syntax:

SPECGRAM(series, len, overlap, fftlen, swin, ampflag)

series

An input series

len

Optional. An integer, the segment length. Defaults to 512.

overlap

Optional. An integer, the number of points to overlap each segment. Defaults to len/2.

fftlen

Optional. An integer, the FFT length. Defaults to len.

swin

Optional. An integer, the windowing function

0:	Hamming
1:	Hanning
2:	Rectangular (none)
3:	Kaiser
4:	Flattop
5:	Blackman
6:	Modified Flattop
7:	Dolph-Chebychev
8:	Taylor
9:	Blackman-Harris

ampflag

Optional. An integer, the window correction method.

0:	do not correct amplitude (default)
1:	correct amplitude
2:	correct RMS amplitude
3:	correct mean-squared amplitude

Returns:

A table of Amplitude values in Frequency vs Time format displayed as an image.

Example:

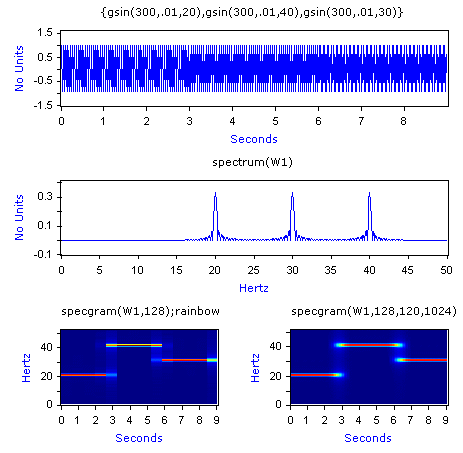
W1: {gsin(300,.01,20),gsin(300,.01,40),gsin(300,.01,30)}

W2: spectrum(W1)

W3: specgram(W1,128);rainbow

W1 consists of three concatenated sinusoids of 20, 40 and 30 Hertz.

W2 shows the frequency spectrum with peaks at 20, 40, and 30 Hertz.

W3 divides W1 into columns of 128 points that overlap by 64 points. The SPECTRUM (i.e. normalized magnitude of the FFT) of each column is calculated and the result is displayed as an image with the rainbow colormap.

The image in W3 shows how the frequency of the series in W1 changes over time, clearly showing the distinct 20, 40 and 30 Hertz components and the times when the components occurred.

Example:

W4: specgram(W1,128,120,1024)

Same as above, but a longer segment overlap is used and the FFT size is zero padded to 1024 points producing a finer resolution image.

$image\specgrampic.gif$

Remarks:

SPECGRAM produces a joint time-frequency amplitude spectrum where the magnitude of the result represents the instantaneous amplitude of the input series at a particular time value.

SPECGRAM divides the input series into segments of length LEN, optionally overlapped by OVERLAP number of points. Each segment is multiplied by an optional window function with optional amplitude correction and the SPECTRUM of each segment is computed. The result in transposed to yield an image with Time along the X axis and Frequency along the Y axis. Each row of a SPECGRAM is a SPECTRUM of the corresponding series segment.

The amplitude specgram is converted to a PSD specgram with:

psdspecgram(s) = deltax(s) * specgram(s)^2 * LEN / 2

where LEN is the specgram segment length. The mean-squared correction factor (3) is appropriate for the window correction of the PSD specgram.

If FFTLEN is larger than the segment length, the segments are zero-padded before computing the SPECTRUM.

Time integration of the un-windowed or amplitude corrected SPECGRAM is approximately equal to the un-windowed or amplitude corrected SPECTRUM of the entire input series, i.e.

colmean(specgram(s)) = spectrum(s) approximately

The SPECTRUM function displays the frequency content of the data where the SPECGRAM functions displays the frequencies and the times at which those frequencies occurs. For example, when applied to music, the spectrum (or FFT) only indicates the notes and the amplitudes of the notes of a given song. The specgram is more like a musical score, displaying the notes, the amplitudes of the notes and the times at which those notes were played.

See DADiSP/FFTXL to optimize the underlying FFT computation.

SPECGRAM

Purpose:

Syntax:

Returns:

Example:

Example:

Remarks:

See Also: