CCEPS

Purpose:

Calculates the complex cepstrum.

Syntax:

CCEPS(series, n)

(c, d) = CCEPS(series)

series	-	An input series or array.
n	-	Optional. An integer, the number of samples to use. If n > length(series), the series is zero padded. Defaults to length(series).

Returns:

A real series or array.

(c, d) = CCEPS(s) returns the cepstrum in c and the lag used to unwrap the phase in d.

Example:

W1: gtri(100, 1, 1/100)^3

W2: W1+delay(W1, 60)/2

W3: cceps(W2)

W4: cceps(W2, 512)

$image\ccepspic.gif$

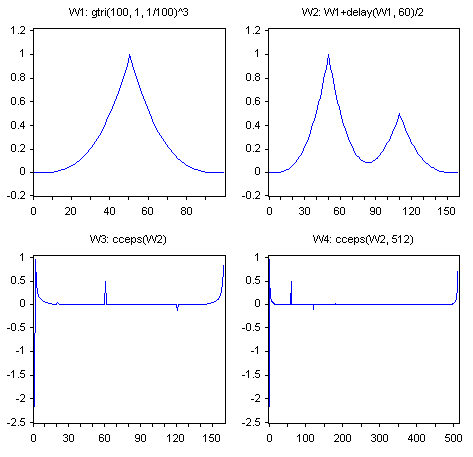
W2 adds a synthesized echo at 60 seconds to the data of W1.

W3 displays a small peak at t == 60 indicating the presence of the echo. W4 performs the same calculation with the data padded to 512 samples.

Example:

W1: {1, -4.0996, 8.4057, -10.1765, 7.7801, -3.5142, 0.7939}

W2: cceps(W1, 1024)

returns the example listed in [2].

Remarks:

The complex cepstrum of a series is essentially ifft(log(fft(s))). However, the complex log calculation requires the evaluation of the continuous phase component. CCEPS unwraps the phase using Shafer's Algorithm. A line is subtracted from the unwrapped phase to remove the integer lag component.

(c, d) = cceps(s)

returns both the cepstrum and the lag used to unwrap the phase such that:

icceps(c, d)

ideally returns s if mean(s) > 0.

CCEPS was tested successfully against the output from [2].

References:

[1] Oppenheim & Shafer

Discrete-Time Signal Processing

Prentice Hall, 1989

pp 788-792

[2] IEEE Press

Programs for Digital Signal Processing

IEEE Press, 1979

Section 7

CCEPS

Purpose:

Syntax:

Returns:

Example:

Example:

Remarks:

References:

See Also: