DADiSP Online Help

Click here to see this page in full context

XYINTERP

Purpose:

Linearly interpolates an XY series to a standard interval series.

Syntax:

XYINTERP(xyseries, interval)

Alternate Syntax:

XYINTERP (xseries, yseries, interval)

Returns:

An interval series, i.e. a series of equally spaced values.

Example:

W1: xy({1, 3, 4, 8}, {1, 2, 3, 2});setsym(square)

W2: xyinterp(w1);setsym(circle)

linearly interpolates the XY series in W1 using the smallest X interval. In this case, the X interval is 1 and the resulting series in W2 contains 8 evenly spaced Y values.

Example:

XYINTERP accepts an interpolation interval, so

xyinterp(W1, .2)

interpolates W1 with an increment of 0.2 resulting in 35 equally spaced values.

Example:

W1: xy({1, 3, 4}, {1, 2, 3})

W2: xyinterp(w1)

W3: xyinterp(w1, 0)

W4: xyinterp(w1, 0.5)

yvals(W1)  == {1, 2, 3}

xvals(W1)  == {1, 3, 4}

W2         == {1, 1.5, 2, 3}

xvals(W2)  == {1, 2, 3, 4}

deltax(W2) == 1.0

W3         == {1, 2, 3}

xvals(W3)  == {1, 2.5, 4}

deltax(w3) == 1.5

W4         == {1. 1.25, 1.5, 1.75, 2, 2.5, 3}

xvals(W4)  == {1, 1.5, 2, 2.5, 3, 3.5, 4}

deltax(W4) == 0.5

W1 contains a 3 sample XY series. W2, W3 and W4 convert the XY series into a regularly sampled interval series.

W2 linearly interpolates W1 to an interval series using an interpolation interval of 1.0, the smallest interval between the original X values.

W3 preserves the original Y values and creates an interval series by dividing the original X range into equal intervals. In this case, the X interval is:

(xmax - xmin) / (length - 1)  = (4 - 1) / 2 = 1.5

W4 linearly interpolated W1 to an interval series using the specified interpolation interval of 0.5.

Example:

XYINTERP also accepts X series and Y series arguments as shown here:

xyinterp(W1, W2, 0.1)

uses the series in W1 as the X values, and the series in W2 as the Y values and linearly interpolates them with an increment of 0.1.

Once an XY series has been interpolated to an interval series, any function can operate on it. For example,

fft(xyinterp(W1)).

Example:

W1: gsin(100, .01, 2)

W2: xyinterp(w1, .005)

W3: interp(W1, 2)

XYINTERP also operates on interval series. W2 is a linear interpolation of the interval series in W1. The results of W2 and W3 are identical to within machine precision.

Remarks:

An series with regularly spaced X values that are monotonically rising (or falling) by a constant X increment such that:

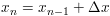
is called an interval series. Because any X value from an interval series can be computed with:

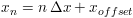
an interval series requires only the DELTAX and XOFFSET values to determine the X values. Thus, for an interval series, explicit X values are not necessary, decreasing the data storage requirements by a factor of 2. Also, because the X values for an interval series are regularly monotonic, speed optimizations for plotting and computations are available.

The X values of the XY series to be interpolated should be monotonic (i.e. either steadily rising or falling). Non-monotonic values are ignored.

As shown, XYINTERP also linearly interpolates interval series.

See XY for a discussion of XY series and interval series.

See XYLOOKUP to find a Y value from an arbitrary X value with possible linear interpolation.

See OUTLIER to replace outlier values with a linear interpolation of the surrounding values.

See RESAMPLE to resample a series to an arbitrary rate.

See Also:

DECILP

INTERPOLATE

OUTLIER

POLYFIT

RESAMPLE

SPLINE

XY

XVALS

XYLOOKUP

XYTAB

YVALS