SPLANE

Purpose:

Displays a Pole-Zero plot of a S-transform.

Syntax:

SPLANE(b, a)

b	-	A series. The numerator (i.e. zero) coefficients in descending powers of s.
a	-	A series. The denominator (i.e. pole) coefficients in descending powers of s.

Alternate Syntax:

SPLANE(z, p, g)

z	-	A series. The zeros of the S-transform.
p	-	A series. The poles of the S-transform.
g	-	A scalar. The gain of the system.

Alternate Syntax:

SPLANE(c)

A series. The system coefficients in cascaded biquad form. If c contains 2 columns, the coefficients are assumed to be in direct form, where the first column is b and the second column is a.

Returns:

An XY series, where each pole is plotted as a light red "x" and each zero is plotted as a black "o".

Example:

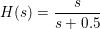
W1: splane({1}, {1, 0.5})

Displays the s plane with a single pole at s = -0.5. The input is given as a system function in descending terms of s.

Example:

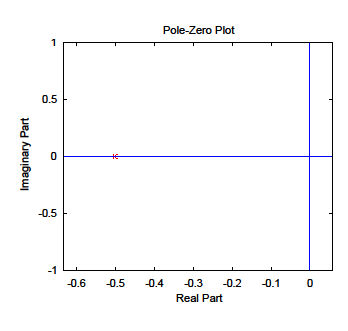
W1: splane({0}, {-0.5}, 1)

Displays the same plot as above. The input is given in terms of zeros and poles.

Example:

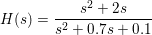
z = roots({1, 2, 0});

p = roots({1, 0.7, 0.1});

splane(z, p, 1);

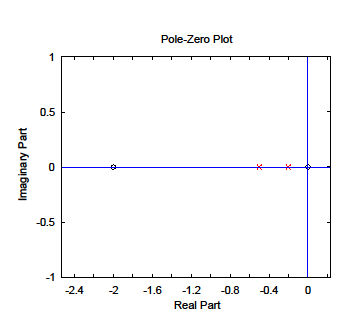
Displays two real poles and two zeros in the current Window. This result is identical to:

splane({1, 2, 0}, {1, 0.7, 0.1})

Remarks:

For splane(b, a), the input series represent the terms of the rational polynomial H(s) = b(s) / a(s) where:

$image\res06.gif$

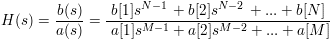
s	=	jω complex frequency
N	=	number of numerator terms
M	=	number of denominator terms

For splane(z, p, g), the gain term must be present, but it does not effect the resulting plot.

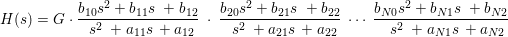
For splane(c), the input c is assumed to be a single column of coefficients in cascaded bi-quad form. This is the output format of analog IIR filters designed by DADiSP/Filters and processed by the CASCADE function.

or equivalently:

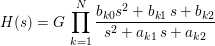
where G is the system gain, b_k and a_k are the filter coefficients for the k^th stage.

If c contains 2 columns, the coefficients are assumed to be in direct form, where the first column is b and the second column is a.

The aspect ratio of the window is set to square to preserve a circular unit circle.

Each pole is plotted as a light red "x" and each zero as a black "o". The unit circle is displayed as a solid circle in the current series color. Axes lines are also drawn through the origin.

Multiple zeros and poles are labeled with a multiplicity number to the upper right of the symbol.

See ZPLANE for a Pole-Zero plot of a discrete system.

SPLANE

Purpose:

Syntax:

Alternate Syntax:

Alternate Syntax:

Returns:

Example:

Example:

Example:

Remarks:

See Also: