
DADiSP Online Help
Click here to see this page in full context

DADiSP Worksheet Functions > Function Categories > Fourier Transforms and Signal Processing > SGOLAYFILT
Filters a series with a Savitzky-Golay smoothing filter.
SGOLAYFILT(x, d, N, w)
|
x |
- |
A series, the input series to smooth. |
|
d |
- |
Optional. An integer or array. If an integer, the Savitzky-Golay polynomial degree. If an array, the explicit Savitzky-Golay coefficients. Defaults to the integer 3, design and process a 3rd order filter. |
|
N |
- |
Optional. An integer, the number of points for the smoothing window. Defaults to |
|
w |
- |
Optional. A series of length N, the weighting factors. Defaults to all ones. |
A series, the result of filtering the input data with the smoothing filter.
W1: gsweep(1000, 1/1000, 1, 50) + gnorm(1000, 1/1000)/5
W2: sgolayfilt(w1)
W3: linavg(w1, 10)
W4: w2;overp(w3, lred)
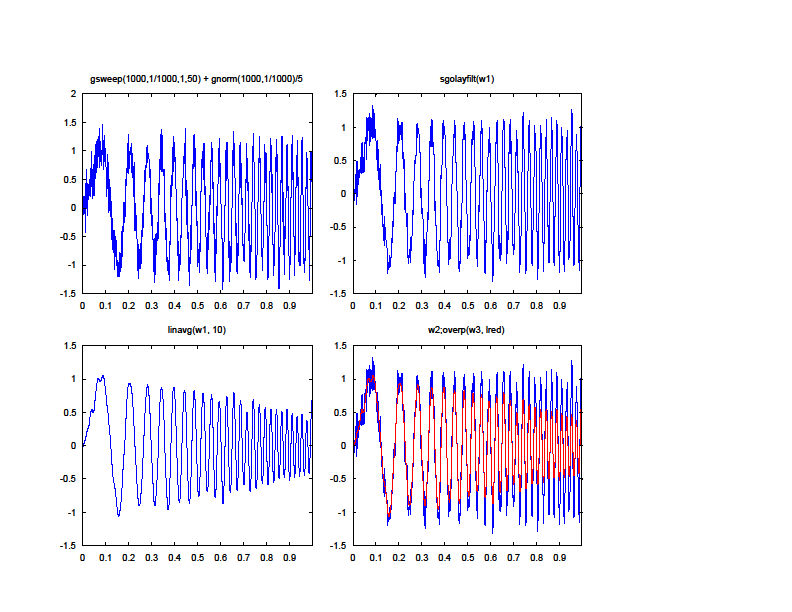
W1 contains 1000 samples of a noisy swept sinewave from 1 Hz to 50Hz.
W2 filters the data in W1 with a 3rd order 5 point Savitzky-Golay filter.
W3 filters the data in W1 with a 10 point zero phase moving average.
W4 graphically compares the two results. The Savitzky-Golay filter more accurately preserves the peak heights of the high frequency oscillations of the input data.
W1: gsweep(1000, 1/1000, 1, 50) + gnorm(1000, 1/1000)/5
W2: sgolayfilt(w1, 3, 11)
W3: linavg(w1, 10)
W4: w2;overp(w3, lred)
Same as above except a 3rd order 11 point Savitzky-Golay filter is used.
W1: gsweep(1000, 1/1000, 1, 50) + gnorm(1000, 1/1000)/5
W2: linavg(w1, 10)
W3: sgolay(3, 11)
W4: sgolayfilt(w1, w3);overp(w2, lred)
Similar to above except the Savitzky-Golay filter coefficients are given as an explicit input array.
Savitzky-Golay filters perform data smoothing and preserve peak resolution by least squares fitting a d order polynomial to an N point sliding window. The data window, N, should be an odd value.
If the filter coefficients are explicit, the window length N and weights w are ignored if provided.
See SGOLAY to generate explicit Savitzky-Golay coefficients.