COSINT

Purpose:

Evaluates Ci(z), the Cosine Integral.

COSINT(z)

A scalar or series, the integration limit.

A scalar or series, the value of Ci(z), the integration of -cos(t) / t from z to ∞.

cosint(1)

returns 0.337404 the value of:

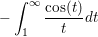
cosint(1 + i)

returns 0.882172 + 0.287249i.

cosint(0..0.01..10);

xlabel("x");ylabel("Ci(x)");label("Cosine Integral");

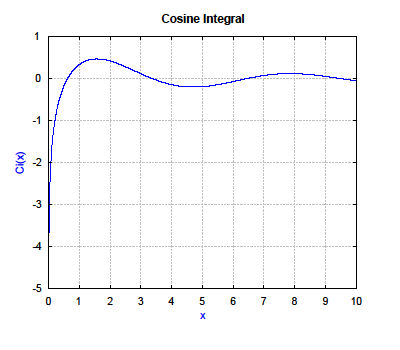
returns 1001 samples of Ci(x) with integration limits from 0 to 10.

W1: 0.01..0.01..10

W2: cosint(W1)

W3: gamm + ln(w1) + integ((cos(w1) - 1) / w1)

W2 contains the cosine integral and W3 computes an approximation by directly integrating (cos(t) - 1) / t.

The Cosine Integral, Ci(z), is defined as:

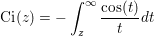
The input z may be complex.

The function can also be computed as:

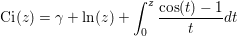
where γ is the Euler constant implemented by GAMM.

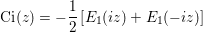
for real(z) > 0 and E₁(z) is the generalized exponential integral implemented by EXPINT.

See SININT to evaluate the Sine Integral.