BANDSTOP

Purpose:

Designs an FIR linear phase bandstop filter.

Syntax:

BANDSTOP(

order, rate, sb1, sb2, ripple, attn, pb1, pb2, "unity_dc")

order	-	Optional. An integer, the filter length. If not specified, the filter order is automatically estimated.
rate	-	A real, the sample rate of the filter in Hertz.
sb1	-	A real, the first stopband edge in Hertz.
sb2	-	A real, the second stopband edge in Hertz.
ripple	-	Optional. A real, the passband ripple in dB. Defaults to 3 dB.
attn	-	Optional. A real, the stopband attenuation in dB. Defaults to 40 dB.
pb1	-	Optional. A real, the first passband edge frequency in Hertz. Defaults to sb1 - 0.05 * rate
pb2	-	Optional. A real, the second passband edge frequency in Hertz. Defaults to sb2 + 0.05 * rate
"unity_dc"	-	Optional. A string, "unity_dc" explicitly sets f(0) to 1.0

Returns:

A series, the bandstop filter coefficients. The filter coefficients are identical to the impulse response of the FIR filter.

Example:

W1: bandstop(1000.0, 200.0, 300.0)

W1 creates a bandstop filter with a sample rate of 1000 Hz and a stopband that extends from 200 Hz to 300 Hz. The first passband defaults to 150 Hz and the last passband defaults to 350 Hz. The resulting filter is 25 samples long with a passband ripple of 1.87 dB and a stopband attenuation of 52 dB.

Example:

W1: bandstop(1000.0, 200.0, 300.0, 3.0, 40.0, 190.0, 310.0)

W2: 20*log10(filtmag(W1, {1}, 1024))

Creates an FIR bandstop filter where the stopband extends from 200 Hz to 300 Hz. The desired passband ripple is set to 3.0 dB and the desired stopband attenuation is 40 dB. The first passband edge is 190 Hz and the last passband edge is set to 310 Hz. The resulting stopband attenuation is 48.0 dB.

Example:

W1: bandstop(1000.0, 200.0, 300.0, 3.0, 40.0, 190.0, 310.0)

W2: gsin(1000, 1/1000, 3) + gsin(1000, 1/1000, 250)

W3: firfilterF(W2, W1)

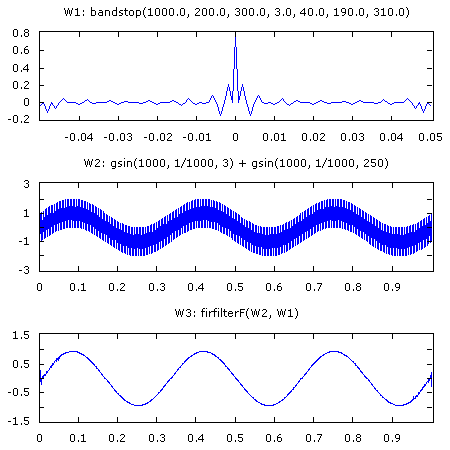
Creates the same FIR bandstop filter as the previous example. W2 contains a series with two sinusoids and W3 applies the filter to recover the lower frequency sinewave.

Remarks:

The BANDSTOP filter specifications are depicted as follows:

The BANDSTOP function uses the Remez Exchange algorithm to compute the FIR filter coefficients. The Remez Exchange algorithm will attempt to meet or exceed the filter specifications with a linear phase FIR filter.

The filter order refers to the number of resulting filter coefficients, though the order will always be odd for a bandstop filter.

The optional "unity_dc" flag guarantees the resulting filter has a frequency response of 1.0 (i.e. 0 dB) at f(0).

The band edges must lie between 0.0 and 0.5 * rate (the Nyquist frequency). Overlapping band edges are not permitted.

See KWBSTOP to design a linear phase FIR bandstop filter with a flat passband using the Kaiser Window method.

See BESSEL, BUTTERWORTH, CHEBY1, CHEBY2 and ELLIPTIC to design IIR filters using the Bilinear Transform method.

BANDSTOP requires the DADiSP/Filters Module.

References:

Oppenheim and Schafer

Digital Signal Processing

Prentice Hall, 1975

Digital Signal Processing Committee

Programs for Digital Signal Processing

I.E.E.E. Press, 1979

BANDSTOP

Purpose:

Syntax:

Returns:

Example:

Example:

Example:

Remarks:

See Also:

References: